The Post-Traumas of the Pandemic on Students: Navigating the Path to Healing
The COVID-19 pandemic has left a profound impact on students, plunging them into a world of post-traumas. Academic disruption, learning loss, social isolation, loneliness, uncertainty, and future anxiety have become their unwelcome companions. The abrupt shift to remote learning, limited resources, and reduced interaction with peers have resulted in significant learning setbacks. Socially, students have experienced a deep sense of isolation, cut off from their support networks and deprived of the usual milestones and celebrations. The uncertainty surrounding the future has added to their burden, with fears of economic hardships and long-term consequences. However, amidst these challenges, the importance of support systems and resilience-building cannot be overstated. Schools, educators, and parents must recognize and address the psychological distress students face. By providing mental health resources, counseling services, and fostering a safe and inclusive environment, students can begin their journey of healing. Equipping them with coping strategies, stress management techniques, and problem-solving skills will enable them to bounce back and thrive. Together, we can navigate the path to recovery and restore hope for a brighter future.
Read moreA Comprehensive Comparative Analysis of IB HL Math Analysis and Approaches (AA) and IB HL Math Applications and Interpretation (AI)
IB HL Math AA and IB HL Math AI are two distinct courses within the International Baccalaureate (IB) Mathematics program. While both courses offer a comprehensive mathematical education, they differ in terms of focus and approach. Math AA is designed to develop students' theoretical understanding of mathematics. It dives deep into topics such as algebra, calculus, and mathematical induction, allowing students to explore the foundations of mathematical theory. Through the study of proofs and logical reasoning, Math AA cultivates analytical thinking and problem-solving skills. This course is recommended for students who have a strong interest in mathematics and intend to pursue further studies in fields such as science, engineering, or mathematics itself. On the other hand, Math AI takes a practical approach, focusing on the application of mathematical concepts in real-world contexts. This course covers topics such as statistics, probability, modeling, and financial mathematics. By emphasizing the practicality of mathematics, Math AI equips students with skills that can be directly applied to various disciplines, including economics, business, and social sciences. Students in Math AI learn to analyze data, make informed decisions, and utilize mathematical models to solve real-life problems. The differences in approach are also reflected in the assessments for each course. Math AA assessments typically involve longer-form questions and proof-based problems, where students demonstrate their understanding of theoretical concepts and their ability to apply them to complex mathematical problems. Math AI assessments, on the other hand, often consist of shorter, context-based questions that require students to apply their knowledge to real-world scenarios and make practical interpretations. When choosing between Math AA and Math AI, students should consider their interests, career aspirations, and university requirements. Math AA is suited for those who have a strong passion for mathematics and plan to pursue mathematics-intensive disciplines in higher education. On the other hand, Math AI is more suitable for students interested in the practical applications of mathematics and pursuing fields where data analysis and modeling play a vital role. It is important for students to carefully evaluate their strengths and future goals when deciding between these two courses. Consulting with teachers, university guidance counselors, and admissions departments can provide valuable insights and help students make an informed decision about which course aligns best with their interests and aspirations. Both Math AA and Math AI offer unique learning experiences and valuable mathematical knowledge, providing a strong foundation for academic and professional success.
Read moreUnleashing Potential with EduIB: A Revolution in Education
EduIB is not just an online learning platform; it is a revolution in education, a beacon of knowledge that illuminates the path to success for learners worldwide. With its vast array of courses, expert educators, and flexible learning environment, EduIB is breaking down barriers and democratizing access to education. It is a platform that believes in the potential of every individual, fostering a community where learners are empowered to reach their full potential. Whether you're a lifelong learner, a professional seeking to upskill, or a student aiming to supplement your studies, EduIB is your partner in the journey of learning and growth. Join the EduIB revolution today, and take the first step towards a brighter, more knowledgeable future.
Read moreUnlocking the Power of Recursive Formulas: A Comprehensive Guide and Examples
"In the realm of mathematical sequences, recursive formulas hold a key to unlocking a world of patterns and calculations. By defining each term in relation to its preceding terms, recursive formulas provide a powerful tool for understanding and predicting the behavior of sequences. In this comprehensive guide, we delve into the intricacies of recursive formulas, exploring their structure and functionality. From arithmetic sequences to the mesmerizing Fibonacci sequence, we unravel the secrets behind these formulas and showcase their applications. Through illuminating examples and step-by-step solutions, you'll gain the insight and skills to navigate and harness the power of recursive formulas. Whether you're a mathematics enthusiast, a student, or a curious mind, this guide will equip you with the knowledge to unravel the hidden patterns and unveil the magic within recursive sequences."
Read moreExploring the Differences between Linear Regression and Least Squares Regression
Linear regression and least squares regression, although related, have unique characteristics that distinguish them in the field of regression analysis. While linear regression aims to establish and quantify the linear relationship between variables, least squares regression focuses on estimating the coefficients that minimize the sum of squared differences between observed and predicted values. Linear regression serves as a versatile statistical technique employed across various domains. Its primary objective is to determine the nature and strength of the linear association between a dependent variable and one or more independent variables. By fitting a straight line to the data, linear regression provides insights into how changes in the independent variables affect the dependent variable. For example, it can be used to predict an individual's income based on their years of education or forecast the demand for a product based on its price. On the other hand, least squares regression is a method used within linear regression to estimate the coefficients that yield the best-fitting line. By minimizing the sum of squared differences between observed and predicted values, least squares regression seeks to find the optimal combination of coefficients that provides the closest approximation to the actual data points. This method takes into account the errors or residuals between the observed and predicted values, aiming to minimize their squared values to ensure an accurate fit. To ensure reliable results, both linear regression and least squares regression rely on certain assumptions. These include assumptions of linearity, independence, homoscedasticity (constant variance), and normality of residuals. Violations of these assumptions can lead to biased coefficient estimates and inaccurate predictions. In practice, researchers and analysts often employ linear regression for its broader scope in exploring relationships between variables, while utilizing the least squares regression technique to estimate the coefficients necessary for constructing the best-fitting line. Understanding the nuances and differences between these two approaches is crucial for accurately interpreting regression models and deriving meaningful insights from data. In conclusion, linear regression and least squares regression play distinct roles within the field of regression analysis. Linear regression focuses on characterizing the linear relationship between variables, while least squares regression is a specific method used within linear regression to estimate the coefficients that minimize the sum of squared differences. By comprehending their disparities, researchers can harness the power of regression analysis to make informed decisions, develop predictive models, and gain valuable insights into the complex relationships among variables.
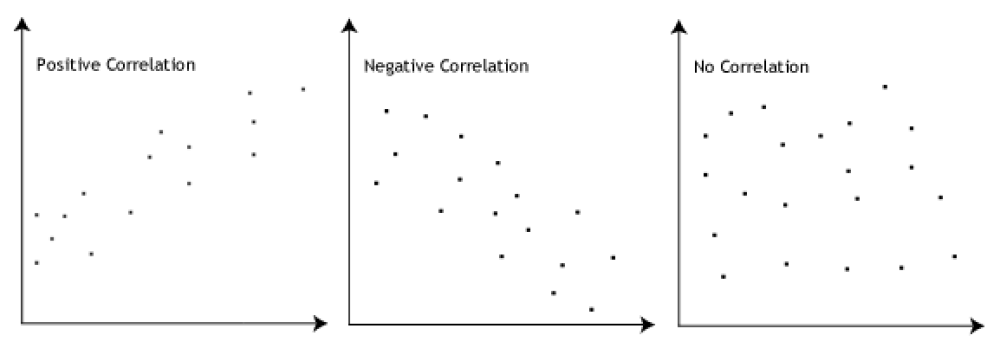
Read moreUnderstanding Linear Correlation: Definition, Use, and Interpretation
Linear correlation is a vital statistical concept that illustrates the relationship between two variables. It quantifies how these variables move in relation to each other, either increasing or decreasing simultaneously (positive correlation), or moving in opposite directions (negative correlation). The linear correlation coefficient, or Pearson's correlation coefficient, measures this relationship, with a value ranging between -1 and 1. Despite the power of this tool in representing the strength and direction of the relationship between variables, it is not without limitations. It is restricted to identifying linear relationships and might overlook other types of relationships such as quadratic or exponential. Moreover, the presence of outliers or confounding variables can influence the correlation coefficient and potentially lead to misleading interpretations. The importance of understanding and correctly interpreting linear correlation cannot be overstated, as it forms the foundation for statistical analysis in a myriad of fields. However, care must be taken to remember that correlation does not imply causation; even a strong correlation does not definitively establish a cause-effect relationship between the variables. Instead, it serves as a preliminary tool for identifying potential relationships that can be further investigated using more complex statistical models.
Read moreMaximizing Summer Break: A Comprehensive Guide for IB Students
The International Baccalaureate (IB) program, renowned for its rigorous academic standards, often leaves students feeling overwhelmed, especially as they approach their final exams. However, the summer break presents a unique opportunity for these students to consolidate their knowledge, fill in gaps, and prepare for the upcoming academic year at their own pace. One of the key resources at their disposal is EduIB, which offers a plethora of study materials, including past papers and subject-specific resources. For instance, students can work through past papers under exam conditions to familiarize themselves with the format and timing of the IB exams. This practice not only helps students identify areas of weakness but also builds their confidence in tackling exam-style questions. In particular, for challenging courses like IB Math SL, students should review key topics such as algebra, functions, and trigonometry, and solve practice problems to reinforce their understanding and improve their problem-solving skills. Additionally, familiarizing themselves with the use of a graphical display calculator is crucial, as it is an essential tool in the IB Math SL course. However, while studying is important, it is equally crucial to balance it with leisure activities to prevent burnout. Engaging in activities that complement their studies, such as reading books related to their subjects of interest or visiting museums, can make studying more effective and enjoyable. In conclusion, the summer break is a golden opportunity for IB students to prepare for their exams. By utilizing resources like EduIB, focusing on challenging subjects like IB Math SL, and balancing study with leisure, students can enhance their knowledge, boost their confidence, and enter the new academic year fully prepared.
Read moreLinear Modeling in IB SL Math AI: Understanding the Basics and Applications
Linear modeling is a crucial topic in IB SL Math AI that involves creating linear equations to represent the relationship between two or more variables. Linear equations are of the form y = mx + b, where y is dependent on x, and m represents the slope of the line, while b represents the y-intercept. Linear modeling has various applications in fields such as physics, economics, and social sciences, where students can use it to make predictions and analyze real-world problems. In this article, we will explore the basics of linear modeling, its applications, and the essential skills required to interpret and analyze linear models. By mastering linear modeling, students can build a strong foundation in mathematics and apply their skills to a wide range of fields and disciplines.
Read moreAmortization and Exponential Functions in IB SL Math AA: Understanding Loan Repayment and Financial Decision-Making
Amortization and exponential functions are important topics in IB SL Math AA as they are used to model the repayment process for loans. By understanding these concepts, students can make informed financial decisions about loans and investments. Exponential functions are used to calculate the interest on a loan over time, which is essential for determining the total amount that needs to be paid back. Additionally, the concept of present value is used to calculate the amount of money that is needed to pay off a loan over time. In this essay, we will explore how exponential functions are used in the context of amortization and how they can be applied in real-world situations.
Read moreTrigonometry Modeling in IB SL Math AA: Applications in Engineering, Physics, and Architecture
Trigonometry modeling is a fundamental concept in IB SL Math AA that has a wide range of applications in various fields, including engineering, physics, and architecture. By applying trigonometric functions and identities to real-world situations, we can model the motion of objects, design structures, and analyze complex systems. One of the essential tools for trigonometry modeling is the unit circle, which allows us to define trigonometric functions in terms of the coordinates of points on the circle. The unit circle is used to model circular motion, such as the movement of a Ferris wheel or the rotation of planets in space. Trigonometry modeling is also crucial in designing structures such as suspension bridges, where the tension in cables must be calculated at specific angles to support the weight of the bridge. By studying trigonometry modeling in IB SL Math AA, students will develop a strong foundation that will prepare them for future academic and professional pursuits in STEM fields.
Read more